Table of contents
- What is Binary Search
- Binary search x Linear search
- Runtime Binary Search
- Implementing Binary Search: Golang
What is Binary Search
Binary search is an algorithm that performs an efficient search to find any item in an ordered list. The way it works is very simple: it divides the list in half (in the part that may contain the sought element) until it reduces the list enough to find the element (or not).
Binary search x Linear search
In 2023, it is estimated that the population of planet Earth will be 8 billion people. Imagine a scenario where we would have to search through all these people on our planet to find an Invisible Cities Architect. Let’s simulate 2 scenarios: linear search and binary search, considering that the order of names in the list is sorted.
Linear Search:
Suppose we create an algorithm to perform a simple search (linear search) in this list with all individuals:
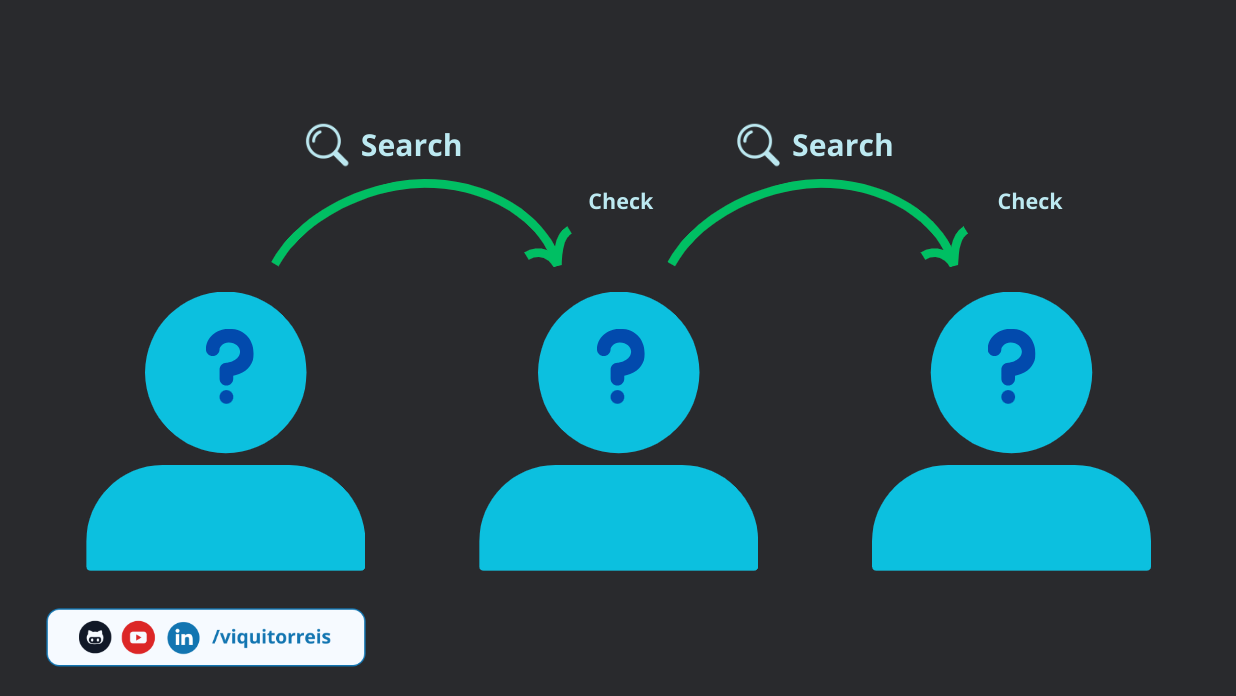
in the worst-case scenario we would have to search through all the people on the list, and based on the assumption that each search + check would take 1 millisecond, the complete search would cost us just over 3 months. That would be too much time; do we have a better solution for this problem?
Better Search Method:
If we start in the middle of the list, that is, at person number 4 billion, we eliminate half the attempts right at the start:

Since the response was that our guess was too low, all elements from the beginning to the middle will be disregarded. Although we missed our attempt, we eliminated half the possibilities.
- In the next guess, we will guess the middle of the remaining part..
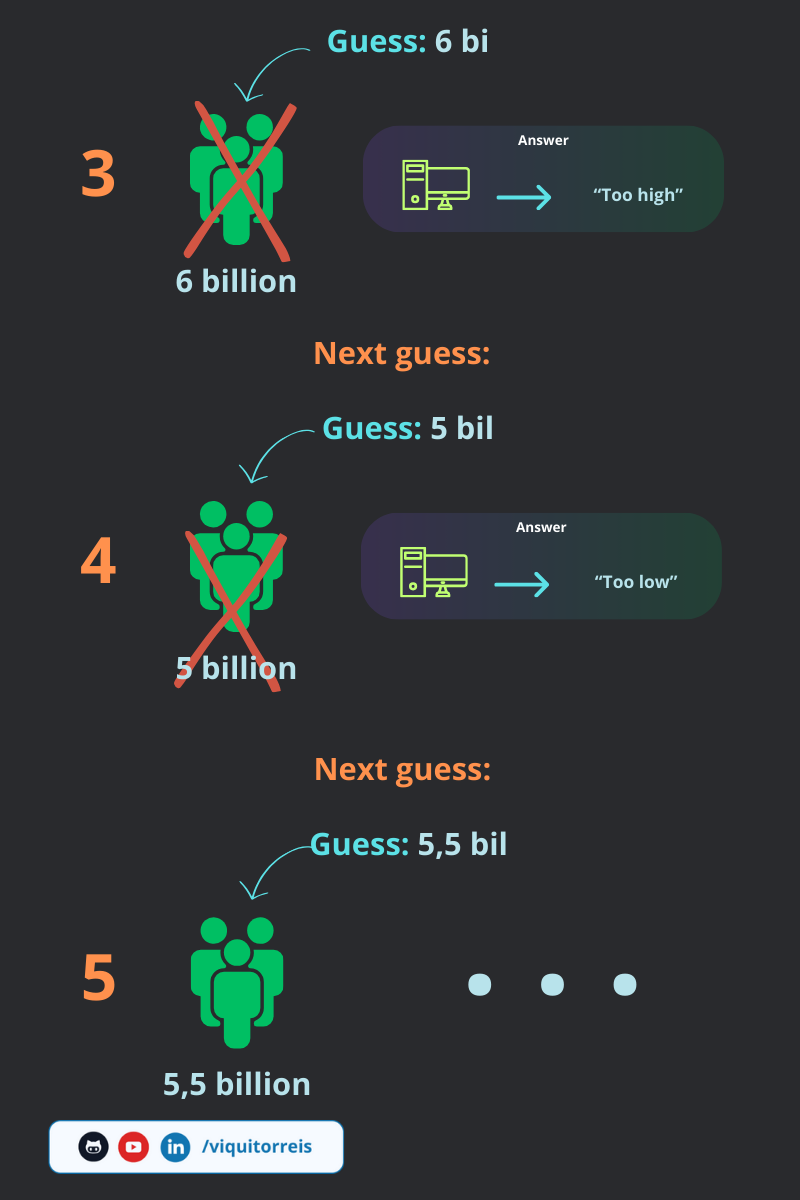
In binary search, we continue this process of dividing the remaining possibilities by half until we find the desired element.
By doing Binary Search, it would take a maximum of 33 searches to find the desired value, if each search = 1 ms, we would spend 33 milliseconds to perform this search.
- Therefore:
- Linear Search => we would spend 3 months on the search
- Binary Search => we would spend 33 milliseconds on the search
Runtime of Binary Search
To calculate how much time the Binary Search may take (in the worst-case scenario - the last element to search for is the one we want), we just need to perform a simple operation. Generally, when we talk about the runtime of algorithms, we almost always calculate the logarithm in base 2:

In our case, the log of 8 billion in base 2 ≃ 33.
Implementing Binary Search: Golang
To implement Binary Search, we can simply follow these steps:
- We need the value of the smallest element and the largest element.
- We loop while the smallest element is less than or equal to the largest, continuing the search (if we don’t find the desired element).
- Get the middle value.
- ‘Guess’ with the middle value.
- If the guess is too low, the smallest element becomes larger than the middle element.
- If the guess is too low, the largest element becomes smaller than the middle element.
- The loop continues until we find the desired element (or not).
- Implementation in Golang:
package main
import (
"sort"
)
func binary_search(item int) int {
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99}
// arr must be sorted...
sort.Ints(arr)
lo := 0
hi := len(arr) - 1
for lo <= hi {
mid := (hi + lo) / 2
guess := arr[mid]
if guess == item {
return mid
}
if guess > item {
hi = mid - 1
} else {
lo = mid + 1
}
}
return 0
}
func main() {
binary_search(7)
}